👉 Đọc lại phần 1 của thuật toán tại https://blog.thanhnamnguyen.dev/tim-hieu-ve-thuat-toan-trong-lap-trinh-phan-1

Ký hiệu tiệm cận?

Phân tích tiệm cận là một kỹ thuật được dùng để xác định hiệu quả của một thuật toán mà không dựa vào các thông số kỹ thuật phần cứng và tránh để thuật toán so sánh chính nó với cách tiếp cận lãng phí thời gian. Với phân tích tiệm cận, ký hiệu tiệm cận là một kỹ thuật toán học được dùng để chỉ ra độ phức tạp thời gian của thuật toán.

Ta có 3 ký hiệu tiệm cận phổ biến như sau:

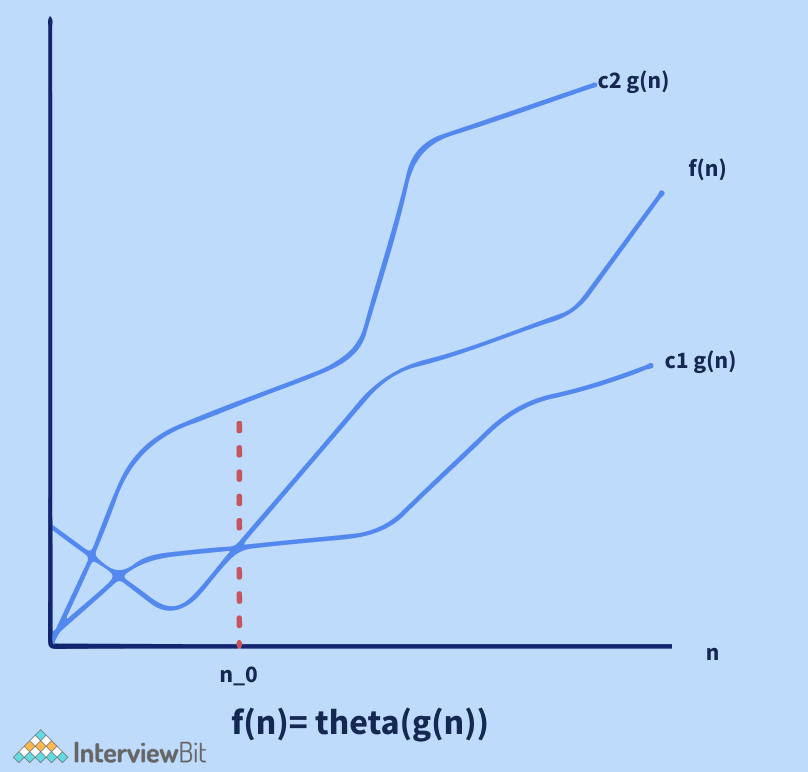
• Ký hiệu theta (θ): dùng để xác định chính xác dáng điệu tiệm cận. Nó liên kết các hàm từ bên trên và bên dưới để xác định dáng điệu tiệm cận. Bỏ qua các số hạng bậc thấp và các hằng số đứng đầu là một cách đơn giản để lấy ký hiệu theta cho một biểu thức.

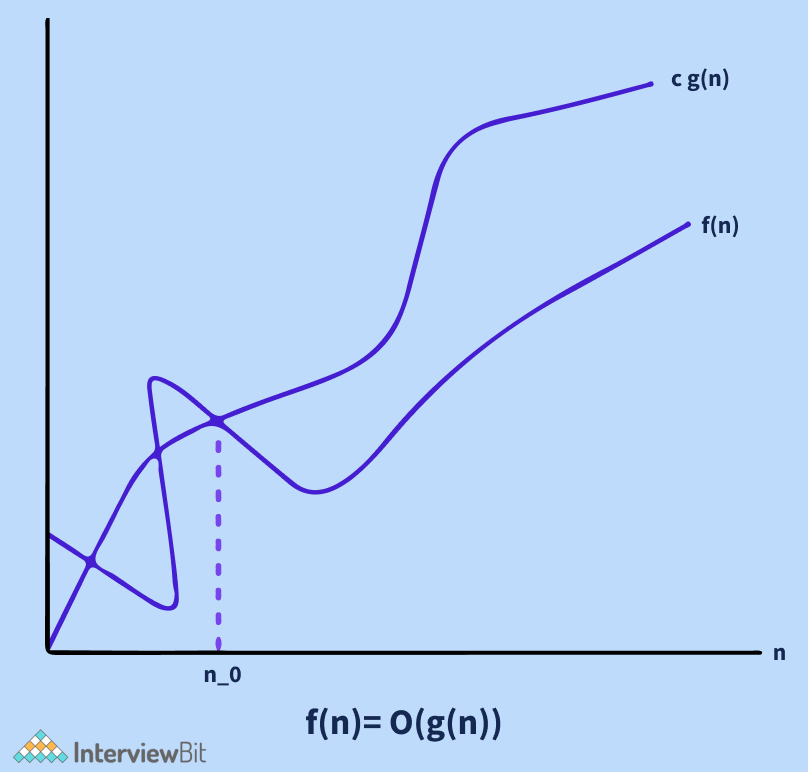
• Ký hiệu O lớn: dùng để xác định cận trên của một thuật toán. Xem xét thuật toán Insert Sort: trong trường hợp tốt nhất nó cần thời gian tuyến tính và trường hợp xấu nhất cần thời gian bậc hai. Insert Sort có độ phức tạp thời gian là (O(n^2)). Nó hữu ích khi ta chỉ có cận trên về độ phức tạp thời gian của thuật toán.

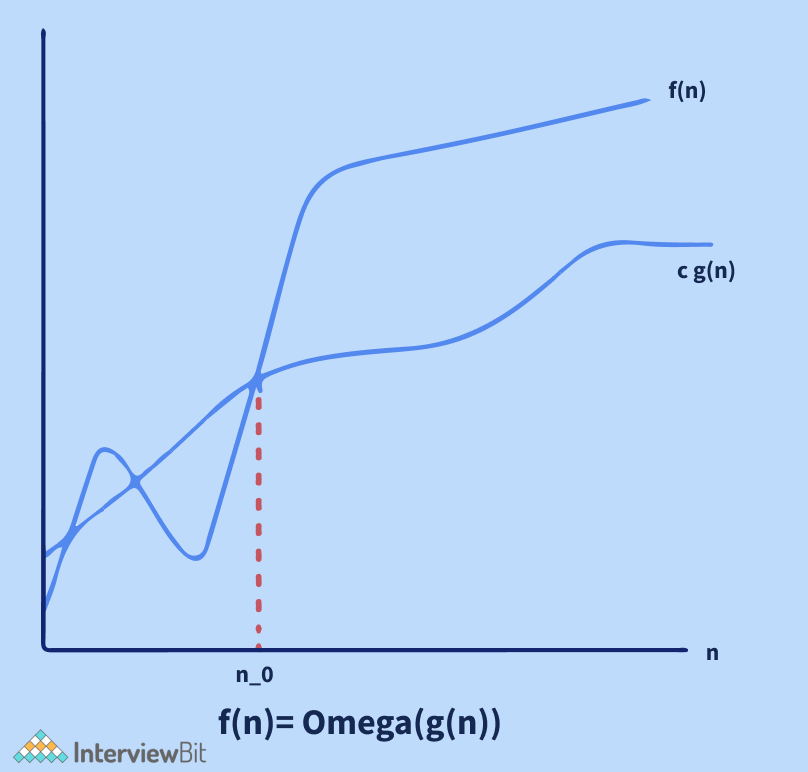
• Ký hiệu omega (Ω): dùng để cung cấp cận dưới cho một hàm, ngược với ký hiệu O lớn. Nó hữu ích khi ta chỉ có cận dưới của độ phức tạp thời gian của thuật toán.

Viết chương trình đổi giá trị hai số mà không dùng biến tạm?

Đây là một câu hỏi thường gặp trong các cuộc phỏng vấn ở nhiều công ty khác nhau. Có nhiều cách để đổi giá trị cho hai số, tuy nhiên ở đây điều kiệu là không được dùng biến tạm. Đối với bài toán này, nếu bạn có thể giải quyết tình huống overflow bạn sẽ để lại ấn tượng tốt với người phỏng vấn.

Giả sử ta có hai số nguyên a và b, với a=5 và b=6 ta cần hoán đổi hai số này mà không cần dùng biến tạm, ta có thể làm như sau:

a = a + b;
b = a - b; // this will act like (a+b) - b, and now b equals a.
a = a - b; // this will act like (a+b) - a, and now an equals b.

Đã xong, nhưng nó có một vấn đề là nếu phép cộng vượt quá giá trị lớn nhất của kiểu int (như Integer.MAX_VALUE trong Java) hoặc nếu phép trừ nhỏ hơn giá trị nhỏ nhất (Integer.MIN_VALUE) thì nó sẽ gây ra hiện tượng overflow.

Phương thức XOR

Để khắc phục vấn đề trên ta có thể dùng XOR, trong các ngôn ngữ như C, C++ hay Java có một toán tử bit là XOR (^).

x = x ^ y;
y = x ^ y;
x = x ^ y;

Mô hình Chia để trị

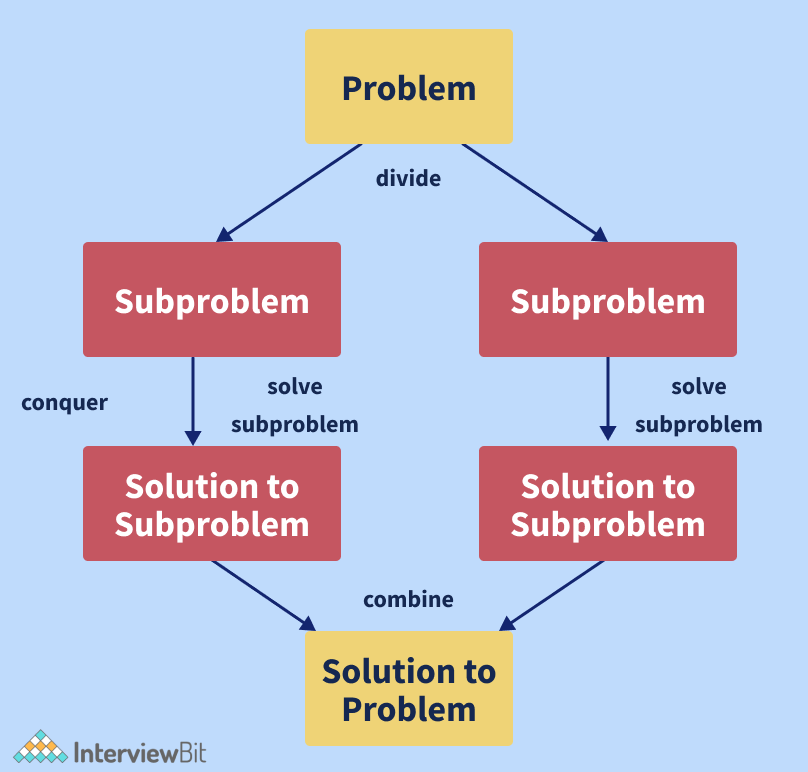
Chia để trị là một mô hình thuật toán, không phải thuật toán. Nó được xây dựng để xử lý một lượng lớn dữ liệu, bằng cách chia nhỏ nó thành từng phần nhỏ hơn và xác định giải pháp cho các phần nhỏ. Nó kết hợp giải pháp của tất cả phần nhỏ thành một giải pháp toàn cục duy nhất. Dưới đây là mô hình của chia để trị:

• Devider: Tách bài toán ban đầu thành một tập các bài toán con.

• Conquer: Giải quyết từng bài toán con đơn lẻ.

• Combiner: Kết hợp giải pháp của các bài toán con thành một giải pháp tổng thể.

Các thuật toán dùng mô hình chia để trị:

• Binary Search

• Merge Sort

• Strassen's Matrix Multiplication

• Quick Sort

• Closest pair of points

Thuật toán tham lam

Thuật toán tham lam là một phương pháp nhằm mục địch chọn ra quyết định tối ưu nhất ở mỗi bước con, cuối cùng dẫn đến giải pháp tối ưu tổng thể. Tức là, tại mỗi thời điểm thuật toán luôn chọn câu trả lời tốt nhất ngay lập tức mà không cần cân nhắc tương lai. Cũng có thể nói thuật toán sẽ chọn ra câu trả lời tốt nhất hiện có, bất kể hậu quả là gì. Các thuật toán tham lam có thể tìm ra câu trả lời không phải là tối ưu nhất trong một số trường hợp.

Các ví dụ sử dụng thuật toán tham lam:

• Prim's Minimal Spanning Tree Algorithm

• Kruskal's Minimal Spanning Tree Algorithm

• Travelling Salesman Problem

• Fractional Knapsack Problem

• Dijkstra's Algorithm

• Job Scheduling Problem

• Graph Map Coloring

• Graph Vertex Cover

Thuật toán tìm kiếm

Thuật toán tìm kiếm được sử dụng để tìm kiếm một phần tử hoặc lấy nó ra từ một cấu trúc dữ liệu (thường là một danh sách các phần tử). Các thuật toán này được chia thành hai loại dựa trên loại hoạt động tìm kiếm:

• Tìm kiếm tuần tự: Phương pháp này duyệt qua danh sách các phần tử liên tục, kiểm tra từng phần tử và báo cáo nếu phần tử cần tìm có được tìm thấy hay không. Tìm kiếm tuyến tính là một ví dụ về thuật toán tìm kiếm tuần tự.

• Tìm kiếm theo khoảng: các thuật toán này được tạo đặc biệt cho tìm kiếm trên các cấu trúc dữ liệu đã sắp xếp. Vì nó hướng đến tìm kiếm ở trung tâm cấu trúc và chia ra thành các khoảng nhỏ, để tìm kiếm mục tiêu. Các loại thuật toán này hiệu quả hơn nhiều so với tìm kiếm tuần tự. Tìm kiếm nhị phân là một ví dụ về tìm kiếm theo khoảng

Thuật toán tìm kiếm tuyến tính?

Để tìm kiếm một phần tử trong một tập hợp phần tử, có thể sử dụng tìm kiếm tuyến tính. Nó hoạt động bằng cách duyệt qua tập phần tử từ đầu đến cuối và quan sát thuộc tính của tất cả phần tử đã đi qua.

Giả sử ta có trường hợp với mảng chỉ toàn số nguyên, ta muốn tìm và in tất cả vị trí của phần tử trùng với một giá trị cụ thể (còn gọi là key trong tìm kiếm tuyến tính). Tìm kiếm tuyến tính hoạt động như sau:

1. Dùng vòng lặp duyệt qua danh sách phần tử đã cho.

2. Với mỗi lần lặp, so sánh giá trị hiện tại với key.

3. Nếu trùng in ra vị trí của phần tử hiện tại.

4. Chuyển đến phần tử kế tiếp nếu giá trị không trùng.

5. Lặp lại từ 1 đến 4 cho đến khi hết danh sách.

Độ phức tạp thời gian của thuật toán tìm kiếm tuyến tính là O(n) trong đó n là kích thước của danh sách các phần tử và độ phức tạp không gian của nó là không đổi, nghĩa là O(1).

Thuật toán tìm kiếm nhị phân?

Để áp dụng tìm kiếm nhị phân trên danh sách các phần tử, điều kiện tiên quyết là danh sách các phần tử phải được sắp xếp. Nó dựa trên mô hình thuật toán chia để trị.

Trong tìm kiếm nhị phân, ta chia khoảng tìm kiếm thành hai phần để tìm trong danh sách đã sắp xếp. Ta bắt đầu bằng cách tạo khoảng trên toàn bộ danh sách. Nếu giá trị của khoá tìm kiếm nhỏ hơn phần tử ở giữa khoảng, thì khoảng đó được thu hẹp về trước, còn không nó sẽ được thu hẹp về sau. Ta tiếp tục thực hiện chia trên các khoảng nhỏ cho đến khi tìm được kết quả. Dưới đây là mô tả thuật toán tìm kiếm nhị phân.

1. x sẽ được so sánh với phần tử ở giữa

2. Trả về nếu x trùng với phần tử ở giữa

3. Ngược lại nếu x lớn hơn, x chỉ có thể ở nữa phía sau của mảng vì mảng được sắp xếp theo thứ tự tăng dần. Ta lặp lại với nữa mảng con phía sau.

4. Nếu như x bé hơn, x chỉ có thể ở nữa phía trước của mảng, ta lặp lại với nữa mảng con phía trước.

5. Nếu các khoảng được chia chỉ còn một phần tử(không thể chia nữa), ta dừng tìm kiếm nhị phân.

Độ phức tạp thời gian của tìm kiếm nhị phân là O(log(n)) với n là kích thước của danh sách phần tử và độ phức tạp không gian là O(1)

... Còn nữa ...

Hãy chờ đón phần tiếp theo của thuật toán nhé.